Design A Combinational Circuit That Generates Output As 1 Use K Map For Boolean Minimization

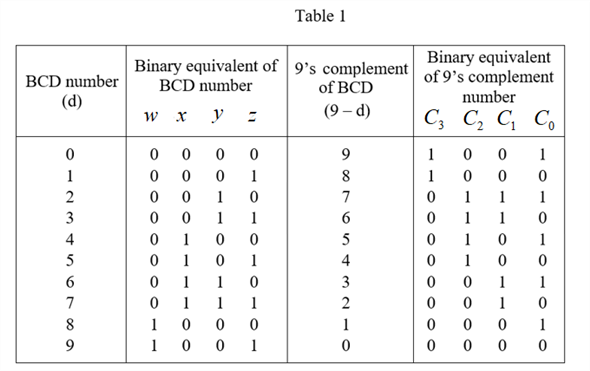
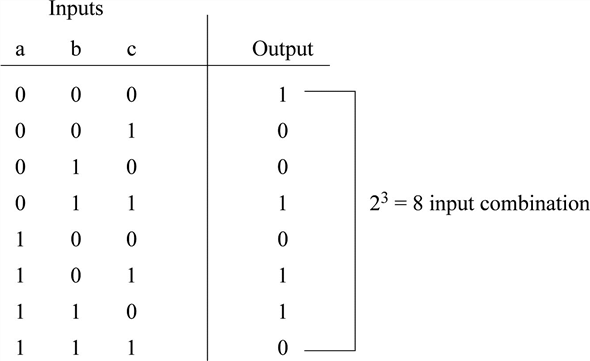
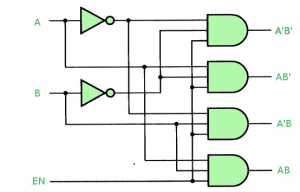
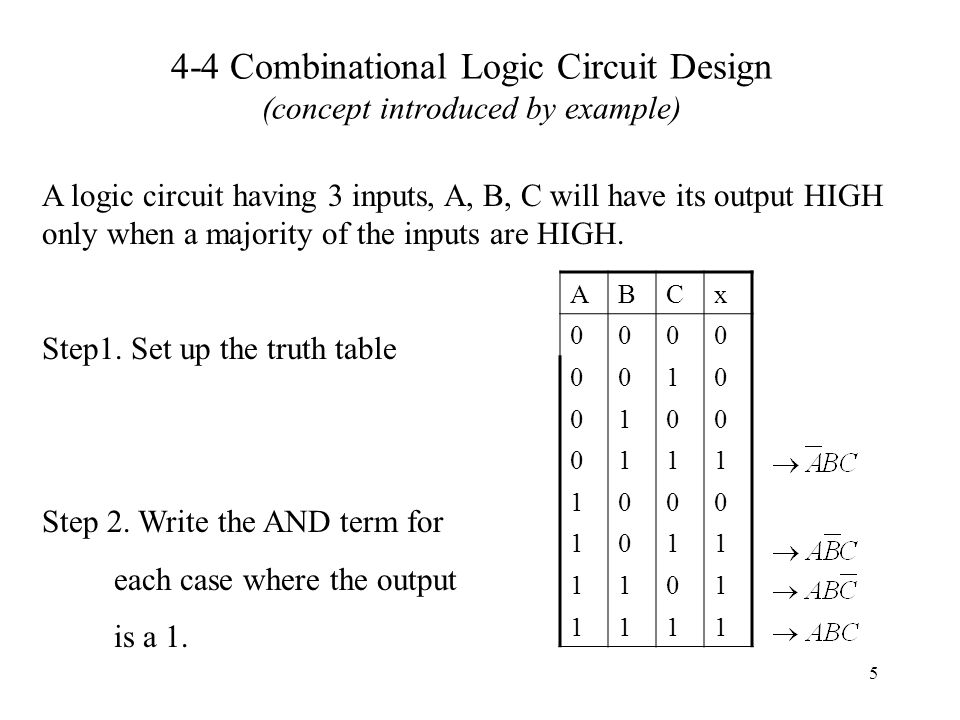
The simplified boolean function for each output is obtained using k map tabulation method and boolean algebra rules.

Design a combinational circuit that generates output as 1 use k map for boolean minimization.

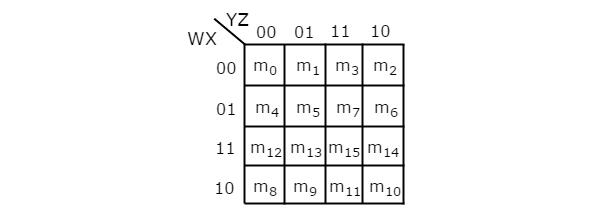
Use karnaugh map to minimise the boolean. From the design specification obtain the truth table from the truth table derive the sum of products boolean expression. The above boolean expression can be implemented by using one ex or gate and one ex nor gate in order to design a 3 bit odd parity generator. To convert a gate circuit to a boolean expression label each gate output with a boolean sub expression corresponding to the gates input signals until a final expression is reached at the last gate.

Questions marks 1 4m design a combinational circuit that generates output as 1 only for particular input pattern student s vtu number use k map for boolean minimization. Example of combinational logic circuit. Combinational logic circuit design. Combinational logic circuits design comprises the following steps.

Understanding this process allows the designer to better use the cad tools and if need be to design critical logic. Minimization using k map the algebraic manipulation method is tedious and cumbersome. The truth table of the odd parity generator can be simplified by using k map as. The k map method is faster and can be used to solve boolean functions of upto 5 variables.

P a b ex nor c. Follow the above listed points to design the logic diagram as per the given statement. Please refer this link to learn more about k map. Example 2 consider the same expression from example 1 and minimize it using k map.

A combinational circuit can have an n number of inputs and m number of outputs. The previous state of input does not have any effect on the present state of the circuit. January 18 2012 ece 152a digital design principles 30 combinational design example 1 design specification design a logic network that takes as its input a 4 bit one s complement number and generates a 1 if that number is odd 0 is not odd label the inputs a b c and d where a is the most significant bit. The output of combinational circuit at any instant of time depends only on the levels present at input terminals.

The output parity bit expression for this generator circuit is obtained as. As you can see the reduced circuit is much simpler than the original yet performs the same logical function. Even though cad tools are used to create combinational logic circuits in practice it is important that a digital designer should learn how to generate a logic circuit from a specification. The logic diagram is drawn.

The combinational circuit do not use any memory. Repeated numbers should consider as single number design a combinational circuit that generates. Next you will learn using guided worked examples how to design combinational logic circuits in minutes.